Giải Toán 9 bài 1 Căn bậc hai
Giải Toán 9 bài 1 Căn bậc hai
Giải SGK Toán 9 bài 1: Căn bậc hai được VnDoc tổng hợp và đăng tải bao gồm hướng dẫn giải chi tiết cho từng câu hỏi và bài tập trong SGK Toán 9 bài 1 Căn bậc hai. Lời giải SGK Toán 9 giúp các các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán lớp 9 hiệu quả. Sau đây mời các em tham khảo chi tiết.
A. Trả lời câu hỏi trang 4, 5, 6 SGK Toán 9 tập 1
Câu hỏi 1 trang 4 SGK Toán 9 tập 1
Tìm các căn bậc hai của mỗi số sau:
a) 9b) c) 0,25d) 2Hướng dẫn giải
a) Vì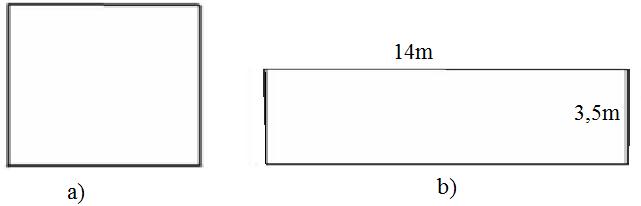 
nên căn bậc hai của 9 là 3 và -3
b) Vì nên căn bậc hai của là và
c) Vì nên căn bậc hai của 0,25 là 0,5 và -0,5
d) Vì nên căn bậc hai của 2 là và
Câu hỏi 2 trang 5 SGK Toán 9 tập 1
Tìm các căn bậc hai số học của mỗi số sau:
a) 49b) 64c) 81d) 1,21Hướng dẫn giải
a) vì
Suy ra căn bậc hai số học của 49 là 7
b) vì
Suy ra căn bậc hai số học của 64 là 8
c) vì
Suy ra căn bậc hai số học của 81 là 9
d) vì
Suy ra căn bậc hai số học của 1,21 là 1,1
Câu hỏi 3 SGK Toán 9 tập 1 trang 5
Tìm các căn bậc hai của mỗi số sau:
a) 64b) 81c) 1,21Hướng dẫn giải
a) Ta có: Căn bậc hai số học của 64 là 8
Vậy 64 có hai căn bậc hai là 8 và - 8.
b) Ta có: Căn bậc hai số học của 81 là 9
Vậy 81 có hai căn bậc hai là 9 và - 9.
c) Ta có: Căn bậc hai số học của 1,21 là 1,1
Vậy 1,21 có hai căn bậc hai là 1,1 và - 1,1.
Câu hỏi 4 SGK Toán 9 tập 1 trang 6
So sánh:
a) 4 và b) và 3Hướng dẫn giải
a) 4 và
Ta có:
Do 15 Leftrightarrow sqrt {16} > sqrt {15} Rightarrow 4 > sqrt {15}" width="281" height="23" data-latex="16 > 15 Leftrightarrow sqrt {16} > sqrt {15} Rightarrow 4 > sqrt {15}" data-i="5" class="lazy" data-src="https://tex.vdoc.vn/?tex=16%20%3E%2015%20%5CLeftrightarrow%20%5Csqrt%20%7B16%7D%20%20%3E%20%5Csqrt%20%7B15%7D%20%20%5CRightarrow%204%20%3E%20%5Csqrt%20%7B15%7D">
Vậy sqrt {15}" width="68" height="23" data-latex="4 > sqrt {15}" data-i="6" class="lazy" data-src="https://tex.vdoc.vn/?tex=4%20%3E%20%5Csqrt%20%7B15%7D">
b) và 3
Ta có:
Do 9 Leftrightarrow sqrt {11} > sqrt 9 Rightarrow sqrt {11} > 3" width="262" height="23" data-latex="11 > 9 Leftrightarrow sqrt {11} > sqrt 9 Rightarrow sqrt {11} > 3" data-i="9" class="lazy" data-src="https://tex.vdoc.vn/?tex=11%20%3E%209%20%5CLeftrightarrow%20%5Csqrt%20%7B11%7D%20%20%3E%20%5Csqrt%209%20%20%5CRightarrow%20%5Csqrt%20%7B11%7D%20%20%3E%203">
Vậy 3" width="68" height="22" data-latex="sqrt {11} > 3" data-i="10" class="lazy" data-src="https://tex.vdoc.vn/?tex=%5Csqrt%20%7B11%7D%20%20%3E%203">
Câu hỏi 5 trang 6 SGK Toán 9 tập 1
Tìm số x không âm, biết:
a) 1" width="60" height="23" data-latex="sqrt x > 1" data-i="0" class="lazy" data-src="https://tex.vdoc.vn/?tex=%5Csqrt%20x%20%20%3E%201">b)Hướng dẫn giải
a) 1" width="60" height="23" data-latex="sqrt x > 1" data-i="2" class="lazy" data-src="https://tex.vdoc.vn/?tex=%5Csqrt%20x%20%20%3E%201">
Ta có: nên 1" width="53" height="17" data-latex="sqrt{x}>1" class="lazy" data-src="https://tex.vdoc.vn?tex=%5Csqrt%7Bx%7D%3E1"> có nghĩa là sqrt{1}" width="67" height="19" data-latex="sqrt{x}>sqrt{1}" class="lazy" data-src="https://tex.vdoc.vn?tex=%5Csqrt%7Bx%7D%3E%5Csqrt%7B1%7D">
Vì nên sqrt 1 Leftrightarrow x > 1" width="149" height="25" data-latex="sqrt x > sqrt 1 Leftrightarrow x > 1" data-i="6" class="lazy" data-src="https://tex.vdoc.vn/?tex=%5Csqrt%20x%20%20%3E%20%5Csqrt%201%20%20%5CLeftrightarrow%20x%20%3E%201">
Vậy x > 1
b)
Ta có: nên có nghĩa là
Vì nên
Vậy
B. Giải bài tập SGK Toán 9 trang 6, 7 tập 1
Bài 1 trang 6 SGK Toán 9 tập 1
Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng 121; 144; 169; 225; 256; 324; 361; 400.
Hướng dẫn giải:
= 11. Hai căn bậc hai của 121 là 11 và - 11.
= 12. Hai căn bậc hai của 144 là 12 và - 12.
= 13. Hai căn bậc hai của 169 là 13 và - 13.
= 15. Hai căn bậc hai của 225 là 15 và - 15.
= 16. Hai căn bậc hai của 256 là 16 và - 16.
= 18. Hai căn bậc hai của 324 là 18 và - 18.
= 19. Hai căn bậc hai của 361 là 19 và - 19.
= 20. Hai căn bậc hai của 400 là 20 và - 20.
Bài 2 trang 6 SGK Toán 9 tập 1
So sánh
a) 2 và b) 6 và c) 7 và .
Hướng dẫn giải:
Viết mỗi số nguyên thành căn bậc hai của một số.
a) 2 = . Vì 4 > 3 nên > hay 2 > .
b) . Vì 36 < 41 nên hay
c) . Vì 49 > 47 nên sqrt{47}" width="82" height="17" data-latex="sqrt{49}>sqrt{47}" class="lazy" data-src="https://tex.vdoc.vn?tex=%5Csqrt%7B49%7D%3E%5Csqrt%7B47%7D"> hay sqrt{47}" width="61" height="21" data-latex="7>sqrt{47}" class="lazy" data-src="https://tex.vdoc.vn?tex=7%3E%5Csqrt%7B47%7D">
Bài 3 trang 6 SGK Toán 9 tập 1
Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương trình sau (làm tròn đến chữ số thập phân thứ 3):
a) X2 = 2; b) X2 = 3;
c) X2 = 3,5; d) X2 = 4,12;
Hướng dẫn: Nghiệm của phương trình X2 = a (với a ≥ 0) là căn bậc hai của a.
Hướng dẫn giải:
Bài 4 trang 7 SGK Toán 9 tập 1
Tìm số x không âm, biết:
a) b) c) d)Hướng dẫn giải
Theo bài ra ta có nên tất cả các căn thức đều xác định.
a.
Do nên bình phương hai vế ta được:
Vậy x = 225
b.
Do nên bình phương hai vế ta được:
Vậy x = 49
c.
Do nên bình phương hai vế ta được:
Vậy
d.
Do nên bình phương hai vế ta được:
Vậy
Bài 5 trang 7 SGK Toán 9 tập 1
Đố. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của hình chữ nhật có chiều rộng 3,5m và chiều dài 14m
Hướng dẫn giải:
Diện tích hình chữ nhật: SHCN = 3,5.14 = 49 (m2)
Gọi a (m) (a > 0) là độ dài của cạnh hình vuông. Suy ra diện tích hình vuông là
SHV = a2 = 49 (m2)
=> a = 7 (m)
Vậy cạnh hình vuông có độ dài là 7m.
C. Ôn lại lý thuyết về căn bậc hai
Căn bậc hai số học
Ở lớp 7, ta đã biết:
Căn bậc hai của một số a không âm là số x sao cho x2 = a.
Số dương a có đúng hai căn bậc hai là hai số đối nhau: Số dương kí hiệu là và số âm kí hiệu là .
Số 0 có đúng một căn bậc hai là chính số 0, ta viết .
ĐỊNH NGHĨA
1. Với số dương a, số được gọi là căn bậc hai số học của a.
Số 0 cũng được gọi là căn bậc hai số học của 0.
Chú ý. Với a ≥ 0, ta có:
Nếu thì x ≥ 0 và x2 = a;
Nếu x ≥ 0 và x2 = a thì
Ta viết xge0" width="159" height="24" data-latex="x=sqrt{a}<=>xge0" class="lazy" data-src="https://tex.vdoc.vn?tex=x%3D%5Csqrt%7Ba%7D%3C%3D%3Ex%5Cge0"> và x2 = a
2. So sánh các căn bậc hai số học
Ta đã biết: Với hai số a và b không âm, nếu a < b thì .
Ta có thể chứng minh được: Với hai số a và b không âm, nếu thì a < b. Như vậy ta có định lí sau đây.
ĐỊNH LÍ
Với hai số a và b không âm, ta có: sqrt{a}<sqrt{b}." width="175" height="27" data-latex="a<b<=>sqrt{a}<sqrt{b}." class="lazy" data-src="https://tex.vdoc.vn?tex=a%3Cb%3C%3D%3E%5Csqrt%7Ba%7D%3C%5Csqrt%7Bb%7D.">
D. Trắc nghiệm Toán 9 bài 1 Căn bậc hai
.........................................
Bài tiếp theo: Giải Toán 9 trang 7 tập 1 bài: Căn bậc hai
Bài liên quan:
- Giải bài tập SBT Toán 9 bài 1: Căn bậc hai
- Bài tập Toán 9: Căn bậc hai
- Chuyên đề Căn bậc hai
Link nội dung: https://topnow.edu.vn/toan-9-bai-1-a67353