Viết phương trình đường thẳng đi qua 2 điểm

Chắc hẳn các bạn học sinh đang gặp rất nhiều vấn đề về phương trình đường thẳng Toán 10: phương trình tham số, phương trình tổng quát của đường thẳng là gì? Cách viết phương trình đường thẳng đi qua hai điểm như thế nào?... đúng không ạ? Để giúp bạn đọc có thể hiểu rõ hơn về vấn đề này, VnDoc xin giới thiệu tới bạn đọc tài liệu hướng dẫn cách xác định và viết phương trình đường thẳng chi tiết giúp các bạn củng cố kiến thức, chuẩn bị tốt cho các kì thi sắp tới!

Bản quyền thuộc về VnDoc.Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

1. Phương trình tổng quát của đường thẳng

Đường thẳng Δ có phương trình tổng quát là: (ax + by + c = 0;left( {{a^2} + {b^2} ne 0} right)) nhận (overrightarrow n = left( {a;b} right)) làm vectơ pháp tuyến.

2. Phương trình tham số của đường thẳng

- Phương trình tham số của đường thẳng đi qua điểm (Aleft( {{x_0},{y_0}} right)) nhận (overrightarrow u (a,b)) làm vecto chỉ phương, Ta có:

(Bleft( {x,y} right) in d Leftrightarrow overrightarrow {AB} = toverrightarrow u Leftrightarrow left{ {begin{array}{*{20}{c}} {x - {x_0} = at} {y - {y_0} = bt} end{array}} right.)

(Leftrightarrow left{ {begin{array}{*{20}{c}} {x = {x_0} + at} {y = {y_0} + bt} end{array}} right.;left( {{a^2} + {b^2} ne 0,t in mathbb{R}} right))

- Đường thẳng d đi qua điểm (Aleft( {{x_0},{y_0}} right)), nhận (overrightarrow u (a,b)) là vecto chỉ phương, phương trình chính tắc của đường thẳng là (frac{{x - {x_0}}}{a} = frac{{y - {y_0}}}{b}) với ((a,b ne 0))

3. Cách viết phương trình đường thẳng đi qua hai điểm

a. Sử dụng định nghĩa

Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.

Phương pháp:

Bước 1: Tính: (overrightarrow {AB} = left( {c - a;d - b} right)) (vectơ chỉ phương của đường thẳng d)

Bước 2: Xác định vectơ pháp tuyến của đường thẳng d: (overrightarrow n = left( {b - d;c - a} right))

Bước 3: Phương trình đường thẳng d:

(left( {b - d} right)left( {x - a} right) + left( {c - a} right)left( {y - b} right) = 0)

b. Sử dụng phương trình tổng quát

Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.

Phương pháp:

Bước 1: Gọi phương trình tổng quát của đường thẳng d là y = mx + n (*)

Bước 2: Thay tọa độ A, B vào phương trình tổng quát ta thu được hệ phương trình ẩn m, n

(left{ {begin{array}{*{20}{c}} {b = am + n} {d = cm + n} end{array}} right. Rightarrow left( {m;n} right) = left( {?;?} right))

Thay m, n vừa tìm được vào phương trình (*) ta suy ra phương trình cần tìm.

4. Bài tập ví dụ minh họa

Hướng dẫn giải

(overrightarrow {AB} = left( {1,1} right))

Phương trình tham số: (frac{{x - 1}}{1} = frac{{y - 2}}{1})

(overrightarrow n = left( { - 1,1} right))

Phương trình tổng quát:

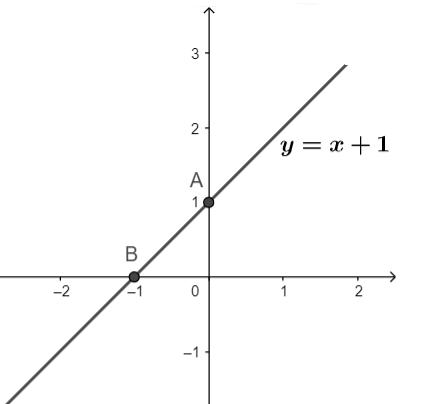
(begin{matrix} - 1.left( {x - 1} right) + 1.left( {y - 2} right) = 0 hfill Rightarrow y = x + 1 hfill end{matrix})

(overrightarrow {AB} = left( {1,1} right))

Phương trình tham số: (frac{{x - 1}}{1} = frac{{y - 2}}{1})

Gọi phương trình tổng quát là:

y = ax + b

Do PTĐT đi qua 2 điểm A, B nên ta có:(left{ {begin{array}{*{20}{c}} {2 = a.1 + b} {3 = a.2 + b} end{array}} right. Rightarrow left( {a;b} right) = left( {1;1} right))

Vậy PT tổng quát cần tìm là: (y = x + 1)

Hướng dẫn giải

a. Gọi phương trình tổng quát là: y = ax + b

Do PTĐT đi qua 2 điểm A, B nên ta có:

(left{ {begin{array}{*{20}{c}} {2 = - 3a + b} { - 4 = 5a + b} end{array}} right. Rightarrow left( {a;b} right) = left( { - frac{3}{4}; - frac{1}{4}} right))

Vậy PT tổng quát cần tìm là: (y = - frac{3}{4}x - frac{1}{4})

Giao điểm của đường thẳng với trục Ox là: (y = 0 Rightarrow x = - frac{1}{3} Rightarrow Aleft( { - frac{1}{3};0} right))

(Rightarrow overrightarrow {OA} = left( { - frac{1}{3};0} right) Rightarrow left| {overrightarrow {OA} } right| = frac{1}{3})

Giao điểm của đường thẳng với trục Oy là: (x = 0 Rightarrow y = - frac{1}{4} Rightarrow Bleft( {0; - frac{1}{4}} right))

(Rightarrow overrightarrow {OB} = left( {0; - frac{1}{4}} right) Rightarrow left| {overrightarrow {OB} } right| = frac{1}{4})

(Rightarrow {S_{OAB}} = frac{1}{2}.OA.OB = frac{1}{2}.frac{1}{3}.frac{1}{4} = frac{1}{{24}})

b. Gọi phương trình tổng quát là: y = ax + b

Do đường thẳng song song với y = -2x + m -1

⇒ a = -2

Phương trình đường thẳng trở thành y = -2x + b

Mà đường thẳng qua điểm A(3; 1)

⇒ 1 = 3.(-2) + b⇒ b = 7

Vậy phương trình tổng quát là: y = -2x + 7

Lời giải

Ta có y' = 6x2 + 6(m - 1)x + 6(m - 2)

Hàm số có cực trị ⇔ y' = 0 có 2 nghiệm phân biệt

⇔ Δ' > 0 ⇔ 9(m - 1)2 - 36(m - 2) > 0 ⇔ 9(m - 3)2 > 0 ⇔ m ≠ 3

Thực hiện phép chia y cho y' ta có phương trình đường thẳng đi qua 2 điểm cực trị là:

d: y = (-m2 + 6m - 9)x - m2 + 3m - 3

Khi đó d song song với đường thẳng y = -4x + 1

-

Trên đây VnDoc đã giới thiệu tới các bạn bài Viết phương trình đường thẳng Toán 10. Bài viết đã gửi tới bạn đọc các tài liệu liên quan về phương trình đường thẳng. Hi vọng qua bài viết này bạn đọc có thêm tài liệu bổ ích nhé.

Mời các bạn cùng tham khảo thêm tài liệu học tập các môn:

• Phương trình tham số của đường thẳng
• Các dạng phương trình đường thẳng
• Câu hỏi trắc nghiệm phương trình đường thẳng
• Bài tập công thức lượng giác lớp 10
• Bảng công thức lượng giác dùng cho lớp 10 - 11 - 12
• Giáo án ôn tập hè môn Toán lớp 10