Cách chứng minh tứ giác nội tiếp Chứng minh tứ giác nội tiếp

Chứng minh tứ giác nội tiếp tổng hợp toàn bộ kiến thức về lý thuyết cách chứng minh dấu hiệu nhận biết kèm theo ví dụ minh họa và các bài tập tự luyện.

Cách chứng minh tứ giác nội tiếp là một trong những bài toán cơ bản trong chương trình lớp 9 hiện hành và thường xuất hiện trong các bài thi vào 10. Qua đó giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập hình học về chứng minh tứ giác nội tiếp. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các bạn xem thêm một số tài liệu như: cách tính bán kính đường tròn ngoại tiếp tam giác, tâm đường tròn ngoại tiếp tam giác.

1. Tứ giác nội tiếp là gì?

Một tứ giác có bốn đỉnh nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

Lúc này, đường tròn được gọi là đường tròn ngoại tiếp, và các đỉnh của tứ giác được gọi là đồng viên.

2. Định lý của tứ giác nội tiếp

Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.

Ngược lại, nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.

3. Dấu hiệu nhận biết tứ giác nội tiếp đường tròn

- Tứ giác có tổng số đo của hai góc đối bằng 180 độ thì tứ giác đó nội tiếp đường tròn.

- Tứ giác có góc ngoài tại một đỉnh bằng với góc trong tại đỉnh đối của nó thì tứ giác đó nội tiếp đường tròn.

- Tứ giác có 4 đỉnh cách đều một điểm mà ta có thể xác định được, điểm đó chính là tâm của đường tròn ngoại tiếp.

- Tứ giác có hai đỉnh kề nhau, hai đỉnh này cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc α thì tứ giác đó nội tiếp đường tròn.

4. Cách chứng minh tứ giác nội tiếp

Phương pháp 1: Chứng minh bốn đỉnh của tứ giác cách đều 1 điểm

Ví dụ: Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E, MB cắt nửa đường tròn (C) tại D (D khác B)

Chứng minh rằng: Tứ giác AMCO và AMDE là các tứ giác nội tiếp đường tròn.

Hướng dẫn giải

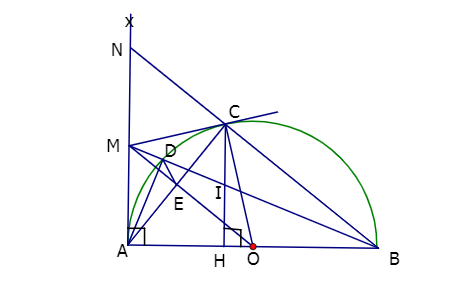
Vì MA, MB, MC là các tiếp tuyến

=> (widehat {MAO} = widehat {MCO} = {90^0})

=> Tứ giác AMCO nội tiếp đường tròn đường kính MO.

Ta có 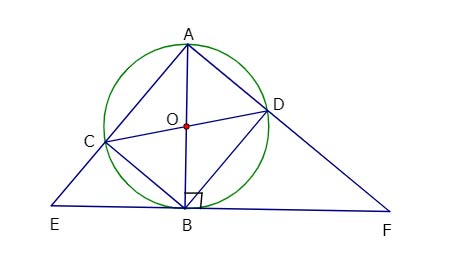(widehat {ADB} = {90^0}) (góc nội tiếp chắn nửa đường tròn)

=> (widehat {ADM} = {90^0}left( * right))

Ta lại có: OA = OC = R, MA = MC

=> MO là đường trung trực của AC

=> (widehat {AEM} = {90^0}left( {**} right))

Từ (*) và (**) => AMDE là tứ giác nội tiếp đường tròn đường kính MA.

Phương pháp 2: Chứng minh tứ giác có hai góc đối diện bù nhau (tổng hai góc đối diện bằng 1800)

Ví dụ: Cho đường tròn (O; R) AB và CD là hai đường kính khác nhau của đường tròn. Tiếp tuyến tại B của đường tròn (O, R) cắt các đường thẳng AC, AD theo thứ tự tại E và F.

a) Chứng minh rằng tứ giác ACBD là hình chữ nhật

b) Chứng minh tam giác ACD và tam giác CBE đồng dạng

c) Chứng minh tứ giác CDEF nội tiếp được đường tròn

Hướng dẫn giải

a) Tứ giác ACBD có hai đường chéo AB và CD bằng nhau và cắt nhau tại trung điểm của mỗi đường, suy ra ACBD là hình chữ nhật.

b) Tứ giác ACBD là hình chữ nhật

=> (widehat {CAD} = widehat {BCE} = {90^0}) (1)

Ta lại có: (widehat {CBE} = frac{1}{2}sd{text{ }}BC;widehat {ACD} = frac{1}{2}sd{text{ }}AD)

Mà sd BC = sd AD (Rightarrow widehat {CBE} = widehat {ACD}) (2)

Từ (1) và (2) => (Delta ACD sim Delta CBE)

c) Vì ACBD là hình chữ nhật nên CB song song với AF

=> (widehat {CBE} = widehat {DFE}) (3)

Từ (2) và (3) => (widehat {ACD} = widehat {DFE}) do đó tứ giác CDFE nội tiếp được đường tròn.

Phương pháp 3: Chứng minh hai đỉnh cùng nhìn đoạn thẳng tạo bởi hai điểm còn lại hai góc bằng nhau.

Ví dụ: Từ một điểm A nằm bên ngoài đường tròn (O; R) ta vẽ hai tiếp tuyến AB và AC với đường tròn (B, C) là tiếp điểm). Trên cung nhỏ BC lấy điểm M, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC)

a) Chứng minh AIMK là tứ giác nội tiếp đường tròn.

b) Kẻ MP vuông góc BC (P thuộc BC). Chứng minh: (widehat {MPK} = widehat {MBC})

Hướng dẫn giải

a) Ta có: (widehat {AIM} = widehat {AKM} = {90^0})

=> Tứ giác AIMK nội tiếp đường tròn đường kính AM.

b) Tứ giác CPMK có: (widehat {MPC} = widehat {MKC} = {90^0})

Do đó CPMK là tứ giác nội tiếp

=> (widehat {MPK} = widehat {MCK})

Vì CK là tiếp tuyến của (O) nên ta có: (widehat {MBC} = widehat {MCK})

=> (widehat {MPK} = widehat {MBC})

Phương pháp 4: Chứng minh bằng phương pháp phản chứng

Có thể chứng minh tứ giác ABCD là một trong những hình đặc biệt sau: Tứ giác ABCD là hình thang cân, hình chữ nhật, hình vuông.

Phương pháp 5: Chứng minh qua góc ngoài của tứ giác

Ví dụ: Cho tứ giác ABCD, nếu chứng minh được góc ngoài tại đỉnh A bằng góc trong tại đỉnh C (tức là góc C của tứ giác đó) thì tứ giác ABCD nội tiếp đường tròn.

5. Bài tập chứng minh tứ giác nội tiếp

Bài tập 1 Cho tứ giác ABCD nội tiếp đường tròn (O). M là điểm chính giữa cung AB. Nối M với D, M với C cắt AB lần lượt ở E và F. Chứng minh tứ giác PEDC là tứ giác nội tiếp.

Bài tập 2: Cho tam gác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiếp.

Bài tập 3; Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm của đường tròn đó.

Bài tập 4: Từ điểm S nằm ở ngoài đường tròn (O) kẻ tiếp tuyến SA; SB với A, B là tiếp điểm và cát tuyến SCD với đường tròn. Gọi I là trung điểm của CD. Chứng minh 5 điểm A, I, O, B, S cùng thuộc một đường tròn.

Bài tập 5: Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E, kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F. Chứng minh:

a) Tứ giác AHCK là tứ giác nội tiếp.

b) AH.AB=AD2

c) Tam giác ACF là tam giác cân.

Bài tập 6:

Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ đường kính AC của đường tròn (O) cắt (O’) tại F. Kẻ đường kính AE của (O’) cắt đường tròn (O) tại G. Chứng minh:

a) Tứ giác GFEC nội tiếp;

b) GC, FE, AB đồng quy.

Bài tập 7: Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kỳ (H không trùng O, B). Trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài đường tròn; MA và MB thứ tự cắt đường (O) ở C và D. Gọi I là giao điểm của AD và BC. Chứng minh các tứ giác MCID và MCHB là tứ giác nội tiếp.